のように「線分を分割した形」は, 分割の比でその形が決定される. これらのように, 何かの形は, その形全体の中で部分部分がどんな割合で配分されるかによって決定される. 「アートとしての数学」トップへ / Haniu files のトップへ
はじめての方や久しぶりの方が見える中,「比」について最近考えていることをお話しした．もともと数列の話しの準備として簡単に触れるつもりだったのだが, 調べる内に大変広がりのあるテーマであることがわかってきた. 「比」とは普通, 数学の概念と考えられているが, 実は, 数学, 言語, 美術, 音楽などに共通する構造性として「広義の比」があり, その「広義の比」が限定された「狭義の比」として数学の比があると私は考えるようになった.
参加者の方々もさまざまに関心を持ってくださり, 用意したメモの途中で終わったので, 次回この続きを行う.
以下に, 今回の話しで進んだ所までのメモを載せておく.
前の数に対して次の数がいつも一定倍になる数列を等比数列という。たとえば,
2, 6, 18, 54, 162, ･･････
なら, いつも 3倍。「等比」数列というとおり,
2 : 6 = 6 : 18 = 18 : 54 = ･･････
となっている。
8, 4, 2, 1, 1/2, 1/4, ･･････
のように, いつも1/2倍になって小さくなってゆく等比数列もある。
さて, このようなどこまでも続く等比数列をあつかう前に, その基礎にある「比」という発想について見ておきたい.
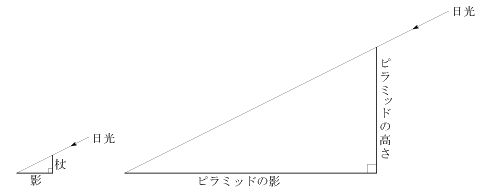
伝説によると, 古代ギリシャ哲学の始祖タレス(紀元前6世紀)は, 杖 1本の助けで, ピラミッドの高さを測ったという. すなわち, 図のように, 日光は一定方向なので, 物の高さと光線と影の作る三角形は, 杖についてもピラミッドについても相似(同じ形)になる. したがって, 杖の影の, 杖の長さに対する比は, ピラミッドの影の, ピラミッドの高さに対する比に等しい. 今の記号で書くと,
(杖の影) : (杖の長さ) = (ピラミッドの影) : (ピラミッドの高さ)
かりに, 杖の影が 2メートル, 杖の長さが 1メートル, ピラミッドの影が 300メートルだったとすると,
2 : 1 = 300 : (ピラミッドの高さ)
から, ピラミッドの高さは150m とわかる.(最大のクフ王のピラミッドは高さ147m)
2つの三角形の相似にもとづき, 「わかるもの」(杖, ピラミッドの影)をもとにして, 「手にとれないもの」(ピラミッドの高さ)を求める. ここに, 相似と比のアイディアの威力が端的に示されている. 誰でも, 地図上で 2 : 1 の距離間隔は, 実物の土地でも 2 : 1 の距離だと判断するのは, 地図が実物と相似(同じ形)の縮小版だからだし, 模型を使って建物の設計をするのも同じアイディアにもとづいている. 相似な形の比によって「手の届かないもの」を知ることは大発見だったはずで, ギリシャ人は相似と比の考え方を発展させて, 地球の周の長さや, 太陽-地球-月の距離比まで推定している.
「手にとれるもの, 身近なもの」を足場に「手にとれないもの, わかりにくいもの」を知る, あるいは表現するという方法は, 数学に限らず人間の思考に欠かせない方法だと思う. たとえば「母なる大地」という表現を支えている構造を解剖すると,
(大地) : (地上の生物) = 母 : 子
(大地の, 地上の生物に対するは, 母の子に対するに等しい)
となるだろうか. 「比喩, たとえ」の表現の多くは, このような「類比」(analogy)と呼ばれる思考方法によっていると思う.
【言葉の歴史】 a : b のような比は, ギリシャ数学では主にロゴス(logos)という言葉で表された. ロゴスの日常語としての意味は, 言葉, 会話, 物語, 報告, 知性などで, 哲学的意味として, 理性や思考があった. 比(ロゴス)という言葉には理性(ロゴス)の意味も重ね合わせてイメージされていたかもしれない
この比(ロゴス)の 2組, a : b と c : d が等しい, すなわち, a : b = c : d であることを, ギリシャ数学ではアナロギア(analogia, 比例)と呼んだ. この数学の述語アナロギアをヘレニズム時代の文法学者が転用し, 類似性などの意味をもつようになった. それを受け継いだのが今日の英語 analogy で, 類似, 類比, 等比, 相似などの意味がある.
ところで, 学校で
6 : 3 = 12 : 6
なら○だが
6 : 3 = 12 : 9
なら×で, その上, 教師はバカにするかもしない. でも, バカにするのは待ってほしい. 6 : 3 = 12 : 9 を
「6と3の関係は, 12と9の関係に等しい」
と読んでみよう. 6才と3才の兄弟の関係は 12才と9才の兄弟の関係と, 3才違いということでは等しい !
もちろん, 「△ : □ = ▲ : ■」とは, △の□に対する倍率と▲の■に対する倍率が等しいということ, と決められているから, 6 : 3 = 12 : 6 だけが○である. 二つ目の式は
6 - 3 = 12 - 9
という差の式に書きなおすと正しい式になる. 2つの数の関係には, 倍率や差などの種類があり, 比は倍率関係で見ているのだ.
ところが, 古代ギリシャ数学の初期のようすを推測すると,「比が等しい」や「比例(アナロギア)」の意味が, もっと広かったことがうかがわれるらしい. 「(6 の 3 に対する関係)と(12 の 9 に対する関係)」のような場合にも, アナロギア(比例)という言葉が使われることがあったようだ. つまり, 関係の種類は問わず,「a の b に対する関係は, c の d に対する関係に等しい」というのが, アナロギア(比例)のもともとの気持ちだったかもしれない. それが, ギリシャ数学の進展の中で今日の意味「前項の後項に対する倍率が等しい」に限定されていったのではないか.
以上は, アルパッド サボー「ギリシャ数学の始源」(玉川大学出版部)によっている.
数学を愛好し尊んだプラトン(紀元前4世紀)は, その思想をしばしば, 数学の形式を利用して語った. ピタゴラス派は数を宇宙の根源と考えたが，その影響を受けているプラトンは, その友人や弟子の数学者を通してギリシャ数学に影響を与えている.
★プラトン(紀元前4世紀)の「線分の比喩」(→「国家」509節c〜参照)
| 見られるもの(可視界) | 思惟によって知られるもの(可知界) | ||
| 似像(間接的知覚) | 実物(直接的知覚) | 悟性的思考(間接知) | 知性的思考(直接知) |
図のように, ひとつの線分が, 見られるもの(可視界)と思惟によって知られるもの(可知界)に 2分されていると思い描く. その2部分をそれぞれ, 先の2分と同じ比例で分割する. つまり, 比の記法で書いてしまうと
似像(にすがた) : 実物 = 間接知 : 直接知 = 可視界 : 可知界
間接知とは, 仮設(前提)から出発して, 始源へさかのぼるのでなく結末へと進んでゆく探求であり, 数学で前提(仮設)から論及し考察の目標に到達するようなものである. これに対し, 直接知とは, 仮説から出発して, もはや仮設でない万有の始源ヘおもむく探求で, 哲学的問答法によって観得されるという.
そして, 上の比例式はたとえば, 間接知の直接知に対する関係は,
似像による知覚の実物による知覚に対する関係と等しい, ということを表している. こうして, 「直接知」という説明しにくいものを類比によって指し示そうとしている.
はじめの杖とピラミッドの例で, 2 : 1 は直角三角形の"形"を決定している. もっと単純な例として, たとえばのように「線分を分割した形」は, 分割の比でその形が決定される. これらのように, 何かの形は, その形全体の中で部分部分がどんな割合で配分されるかによって決定される.
【言葉の歴史】ギリシャ語のアナロギア(比例)のラテン語訳が proportio(関係, 調和, 比例)で, それが英語で proportion(割合, 釣り合い, 比例, 部分)となる. portio は部分の意味. ギリシャ語のアナロギアとくらべると, proportion は, 調和や均衡の意味の比例を表す言葉になっている.
すると, 調和のとれた配分比が調和のとれた形を生むと考えられることになる. たとえば,「線分の分割の比」としては, 古来, 黄金分割(1 : φ = 1 : 約1.618)が, 特に調和のとれた比と考えられ, 多くの彫刻, 建築, 絵画に使われてきた. 黄金分割サンプル
注. 「黄金分割(golden section)」は近代の呼び名で, 古代ギリシャでは単に「分割(section)」と呼ばれ, ユークリッドの原論では「線分の外中比」として現れる.
一定の比が形を決定するということを, 音楽の音の高さに見ることもできる. たとえば, ドレミファソラシドという音の動きは, 歌いはじめの音の高さが違っても, つづく一連の音の高さの比(振動数比)が同じならば, 同一のメロディーとして聞こえる. つまり, 一連の音の高さの比(振動数の比)が特定のメロディーや音階という形を作る.