「アートとしての数学」トップへ / Haniu files のトップへ

「アートとしての数学」第40回(2007/5/26)メモ

石鹸膜が作る形

シャボン玉はまん丸く宙に浮かぶ。なぜ, 四角や三角でなく丸くなるのか ? 針金で輪を作り, 石鹸液につけて引き上げると 平面の膜ができる。この針金の輪を折り曲げて, 横から見ると U字形にしてから膜を張らせると, 「馬の鞍」の形ができる。写真は石鹸膜の替わりに樹脂膜を張らせて固めたもの。

これらの石鹸膜の形に共通することは, 「与えられた条件の下で, 膜の面積ができるだけ小さくなるように膜が張る」ということである。針金, 指, 糸, 板, 棒などを使って石鹸膜を張らせると, さまざまな形ができるが, いずれも, それぞれの条件下で膜面積極小になる。また, このような面積極小の造形や, メカニズムは違うかもしれないが膜造形となぜか似ている形は, 自然界, 人工物を問わず多く, アート作品としての造形にもきわめて刺激される点が多い。そうした観点から, 以下に石鹸膜の各種造形から若干を挙げる。

• シャボン玉。内部に一定体積の空気が閉じ込められているという条件の下でできる形。
  真空中ではシャボン玉はできないはず。
  机の上にシャボン玉を作るとどんな形になるか ?
  (大きく張るシャボン液の作り方。合成洗剤 : 洗濯のり(ポリビニルアルコール) : 水 = 1 : 5 : 10)

  参考。長さ一定のひも 1本で土地を囲み, できるだけ大きい面積を囲むにはひもをどんな形にするとよいか ?
  (カルタゴを作った女王ディドの話。中世ヨーロッパの城壁都市の形。)

  (シュタイナーのちょうつがいによる証明)
• 指に張る石鹸膜。
  指の輪で石鹸膜を張り, それを, 2人でつなぎ大きな膜にする。3人, 4人 ・・・と大きくできるか ?
• 針金枠に張る石鹸膜の形。一枚膜の場合
  平面上の輪に張る膜。
  輪を折り曲げ横から見ると U 字形にすると, 鞍形。
  (平均曲率 0 の形)
  メビウス輪状の膜を作る針金枠の作り方。
  (このタイプは次回にくわしく。写真はこちらにたくさん)
• 針金枠に張る石鹸膜の形。複数の膜が交線を作る場合。
  正四面体の針金枠に張る石鹸膜 → 放散虫の一種 Callimitra の骨格と似ている。 下図は, ヒルデブラント, トロンバ著「形の法則」(東京化学同人)よりスキャン。
  
  

  Callimitra のスケッチと写真 Callimitra Callimitra carolothae Callimitra Callimitra
  次のは, 放散虫の研究でも知られるエルンスト ヘッケル(1834-1919)の生物画。Kunstformen der Natur (1899-1904)
  次のは, Scott Draves氏による, ヘッケルの絵を元にした作品らしい。これらの絵はヘッケルについてのこのページによると放散虫類らしい。この方面は不案内で「らしい」が多くごめんなさい。

• 針金枠と糸。
  平面上の輪に石鹸膜を張ってから, 膜の上に糸の輪をそっと乗せ, 糸輪の内側の石鹸膜を棒などでつついてはじく。すると, 糸輪はどんな形になるか ?
  
• 糸(ロープ)と棒。
  テントの形。フライ・オットーの建築。 フライ オットーは多くの建築を石鹸膜実験を元に設計している。
• 平行な2枚の板とその間の柱でできる膜の形。

  3つの都市の間を石油の輸送ラインで結びたい。工事費を最小にするため, ラインの長さの合計を最小にしたい。ラインをどんな形にするとよいか ?
  もっとたくさんの都市ならどうか ?
  (シュタイナー問題)

  上記の問題に, 平行板の石鹸膜で答えを探せる。
  2枚の板を平行でなくすると膜の形はどうなるか ?
  
• 平行な2枚の板。柱なし。
  写真は2枚の平行なプラスチック板(間隔約4mm)にはさまれた石鹸膜。2007年4月16日撮影。
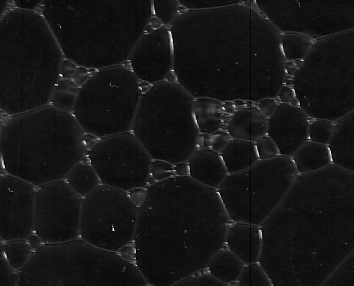  蜂の巣, トンボの羽などと類似。

参考文献 次の本は石鹸膜造形に限らず極小問題について扱っているが, 美しい絵や写真が多く大変親しみやすく, 数学や物理の内容についてもできるだけ入っていきやすい文章で質の高い内容を紹介している。
ヒルデブラント, トロンバ著「形の法則」東京化学同人