トップページへ

分割を早める

何等分にでもできる方法の変形で, 細かい分割をより早く可能にする方法.

【ルール】ナイフと糸だけを使ってケーキやようかんを等分割するための方法を考える. 次のルールを課す. 【手順】

平行四辺形 を, まず, 対角線の一方で切って となる. (以下, ケーキが切られているか離れている場合は図では白線)

切った対角線をはさむ 2頂点を結ぶ直線を，糸をピンと張ってつくり, 次の図のようにアトをつける．（以下, 糸でアトをつけただけの線は図では黒線）すると, はじめの対角線は 2等分される.
ならべかえて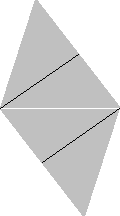
新しい形の平行四辺形の図で白い対角線をはさんで, 上下おのおのに頂点と2等分点が計 2個ある. 糸でこれらの点を次のように結ぶと, 白い対角線は 3等分される. ただし, 糸の線(図で黒線)が混雑してくるので, 以下, 説明に必要な線だけ残して記す.
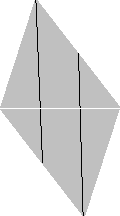ならべかえて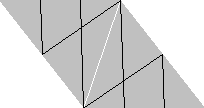
上のならべかえは, 新しい平行四辺形のとなりあう 2辺にそれぞれ 2等分点と 3等分点があるように行った.
白い対角線をはさんで, 左右の三角形のそれぞれに頂点と辺の等分点が計 5個ある. 糸でこれらの点を次のように結ぶと, 白い対角線は 5等分される.
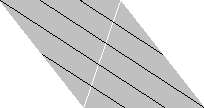ならべかえて
上のならべかえは, 新しい平行四辺形のとなりあう 2辺にそれぞれ 3等分点と 5等分点があるように行った. これらの等分点を利用すれば, この平行四辺形の, 3等分, 5等分, あるいは, 3×5=15等分が次の図のようにできる.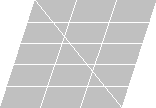
もっと細かい分割に進む場合. 白い対角線をはさんで, 左右の三角形のそれぞれに頂点と辺の等分点が計 8個ある. 糸でこれらの点を次のように結ぶと, 白い対角線は 8等分される.
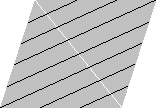ならべかえて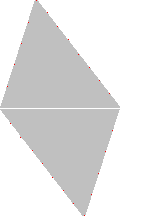
等分点を使えば 5等分, 8等分, あるいは 5×8=40等分が可能. さらに, 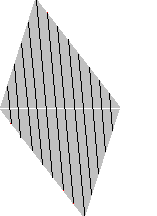で対角線は13等分された. ならべかえて, 平行四辺形のとなりあう 2辺が8等分と13等分されているようにする. ･･････

以下, 同様にして, 平行四辺形の2辺と対角線を, 次々に, 8+13=21等分, 13+21=34等分, 21+34=55等分, ･････････ としてゆける. その途中で縦横に切れば, 8×13=104等分, 13×21=273等分, 21×34=714等分, ･･････ ができる.

<注> 上のように前の 2数をたして次の数ができるような数列(数の並び)を, 1, 1 からはじめると,

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, ･･････

となるが, これはフィボナッチ数列と呼ばれている.

一般には, 平行四辺形のとなりあう2辺がそれぞれ m等分割と n等分割されていると, 対角線が m+n等分割できる. 上では分割数を早くしようとしてフィボナッチ数列が現れたが, m や n には, それまでにその辺にできた分割数は何でも使えるので, もっと自由な分割の増やし方ができる.

対角線等分割の3次元版

上の方法の 3次元版ができることもわかったが, 実際のケーキ切りに試すとケーキがこなごなボロボロになってゆくだけだろう. 理論的にはおもしろいので, 簡単に書いておく.

平行六面体の3方向の辺がそれぞれ, p等分割, q等分割, r等分割されているとする.

<例> p=4, q=3, r=2 の場合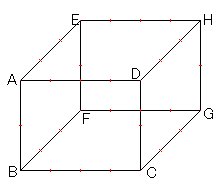

平行6面体の対角線のまわりに位置するこれらの等分割点と頂点を使って, 平行6面体を平面切りして, 対角線を p+q+r等分割することができる.

<例> p=4, q=3, r=2 の場合 まず, 頂点Hから3辺にそって隣にある分割点, 計3個を通る平面で切る. 次にさらに3辺を進み次の分割点2個と頂点Gの計3点を通る平面で切る. 次は頂点Dと3辺の次の分割点3個の計4点を通る平面で切る.･･････ というぐあいで続けると, 直方体はたがいに平行で等間隔の8平面で切られて, 対角線HBは4+3+2=9等分割される.

次にこの平行6面体を適当に切って配置変えすると, 先の(p+q+r)等分割された対角線が外に出るような形にできる.

p=q=r=1の場合からはじめて, 上の過程をくりかえしできるだけ早く分割数を増やすと,
1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, ･･････ となってゆく. 3方向に切れば, たとえば, 9×17×31=4743等分割などができる.