「アートとしての数学」トップへ / Haniu files のトップへ

講座「アートとしての数学」第23回(2005/2/24木)メモ

2項関係の分割と積み上げ

音楽の音程を例に取って言うと, 1オクターブを作る 2音の間をどう分割するかが音階を作り, 他方, オクターブという2項関係を積み上げて次々に高いオクターブができてゆく.

人間の耳は理屈の前に, 男声のドとミの音程と, 女性の1オクターブ高いドとミとの音程を, 同じ音程として感じ取ってきた. それを,
ド : ミ = 高いド : 高いミ
と記せる. これと同時に, ドと高いドの音程は, ミと高いミの音程と等しく, その音程はオクターブと呼ばれている.
ド : 高いド = ミ : 高いミ
このように, ド, ミ, 高いド, 高いミ, の4音は, 2重の等音程に支えられて感じ取られている。
また, この2本の等式は, 数の比において, たとえば,
3 : 5 = 6 : 10
ならば
3 : 6 = 5 : 10
でもあるのと同様である.

等比数列

比の累積(二項関係の再帰的積み上げ)によって 2項関係は無限に多くの項まで広がる. こうしてできる無限数列を等比数列と呼んでいる.

第20回メモから以上までの「比」の話しは, そもそも等比数列の準備のつもりで始めたのだが, 見えてきた「比=2項関係」の意味が, ほとんどそのまま等比数列の意味だろう.

等比数列の漸化式表現

例として, 3から始まり, 前の項に対し次の項がつねに 2倍になる数列,
3, 6, 12, 24, 48, 96, ･････ ☆
を考える.第1項 3をa₁ 第2項 6をa₂ 第3項 12をa₃ ･･････ としよう.
a₂=2a₁
a₃=2a₂
a₄=2a₃
･･・･･
なので, これらをまとめて
a_n+1=2a_n ★
と表せる.すなわち, 第n+1項は第n項の2倍ということ.
★のように, 数列の近所どうしの項の関係式を漸化式(ぜんかしき)という.
等比数列☆は,
第1項(初項)の値, a₁=3 と
漸化式 a_n+1=2a_n ★
とで, 完全に決められる.この 2本の式ははじめに書いた「3から始まり, 前の項に対し次の項がつねに 2倍になる」ということ以上何も言っていない.この2本の式だけから, 3, 6, 12, 24, 48, 96, ･････ ☆という数をイモヅル式に書いてゆけるから, この2本の式が, 数列☆を決定するといえる.あるいはこの2本の式が数列☆を定義している, と言う.

他の数列の漸化式表現

初項が 1で 2ずつ増える等差数列
1，　3， 5， 7， 9， 11， 13， ････
ならば, 漸化式は a_n+1=a_n+2

初項と第2項が1で, つねに, 前の2項をたすと次の項になる数列,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ･････
はフィボナッツィ数列と呼ばれている.この数列の漸化式は,
a_n+2=a_n+1+a_n ▲
ところで, 先に見た等比数列 3, 6, 12, 24, 48, 96, ･････ ☆の漸化式 a_n+1=2a_n ★を,
a_n+1=a_n+a_n ★
と書いて見ると, フィボナッツィ数列の漸化式とよく似てくる.

漸化式▲はそのまま, 2人またりさまの数列の漸化式である.(数の世界のまたりさま参照) ただし, またりさまでは 1+1=0 になるので, 初期条件を 1, 1, とすると,
1, 1, 0, 1, 1, 0, 1, 1, 0, 1, ･･････
となる.フィボナッツィ数列の各項が, 奇数なら1, 偶数なら 0 に変わったと考えられる.
8人またりさまの漸化式は,
a_n+8=a_n+7+a_n

一般に, 漸化式とは次の項を求める手順を示すものだから, 「前の項に対し次の項がつねに 2倍になる」のように普通の言葉で言えばとてもわかりやすい. だから, 漸化式の数式表現がわからなくても"またりさま"はできる. したがって, このような漸化式の手順明示性は, 芸術や工芸ヘの適用に大きな可能性があるし, 手作業と数学とコンピューターの共通の技術的基盤を示しているだろう.

等比数列の一般項表現

数列,
3, 6, 12, 24, 48, 96, ･････ ☆
の別の表現法について.
a₁=3
a₂=3×2
a₃=3×2×2=3×2²
a₄=3×2×2×2=3×2³
a₅=3×2×2×2×2=3×2⁴
･･････ となってゆく.では, a₁₀₀を同様の形の式で書くとどうなるか ?
a₁に2を何回かけたらa₁₀₀になるか考えてみると, 99回ですね. (100人の人がバケツリレイすると, バケツは何回手渡されるか? と同じ) だから,
a₁₀₀=3×2×2×･･････×2=3×2⁹⁹
これらの式をまとめると, a_n=3×2^n-1 ◆
これが数列☆の第n項(一般項ともいう)を表す式である. ◆も 数列☆を決定する式である.
漸化式表現が, 1歩ずつたどるのに対して, 一般項の式表現は, 項数nの入力に対して項の値a_nをすぐ出力してみせようとする. 一般項表現の別の一例を示そう. フィボナッツィ数列の一般項は

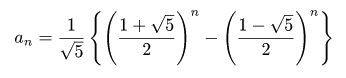
である. この式はワリとすっきり導く方法があり, それがわかると見かけほど複雑には思えなくなる。（導出過程は省略）それでも「前の2項をたすと次の項になる」という漸化式の親しみやすい手作業性とは違って見える.